On the journey of
[논문읽기] Wasserstein GAN 본문
https://arxiv.org/pdf/1701.07875.pdf
Introduction
기존의 GAN 계열에서는
- Unsupervised Learning(또는 Self-Supervised Learning)에서 학습 데이터x에 대한 정답 라벨 y가 존재하지 않기 때문에, 데이터 x의 분포 P(x)를 직접 학습한다.
- P(x)의 파라미터 theta(세타)를 아래와 같이 정의한다.

- P(x)를 직접 표현하는 것은 어렵다.(정답을 이미 알고 있다는 의미)
- 따라서 latent variable z의 분포를 가정하여 입력으로 사용
- Discriminator와 Generator 간의 관계를 학습 시켜 Generator의 분포를 P(x)에 가깝게 학습시킨다.
GAN의 문제점 : Discriminator와 Generator 사이의 균형을 유지하며 학습 시키기 어려움
- Wasserstein GAN의 제안: Discriminator 대신 새로 정의한 critic 사용
- critic : Earth Mover(EM) distance로부터 얻은 scalar 값
- EM distance : 확률 분포 간의 거리 측정 측도
- KL divergence 대신 사용
WGAN의 장점
- training 시, discriminator와 generator간의 balance를 모니터링 하지 않아도 된다.
- GAN에서 일반적으로 발생하는 mode dropping(mode collapse) 해결
- Generator가 Discriminator를 속이기 위해 한 숫자만 생성 (다른 분포 mode는 drop)
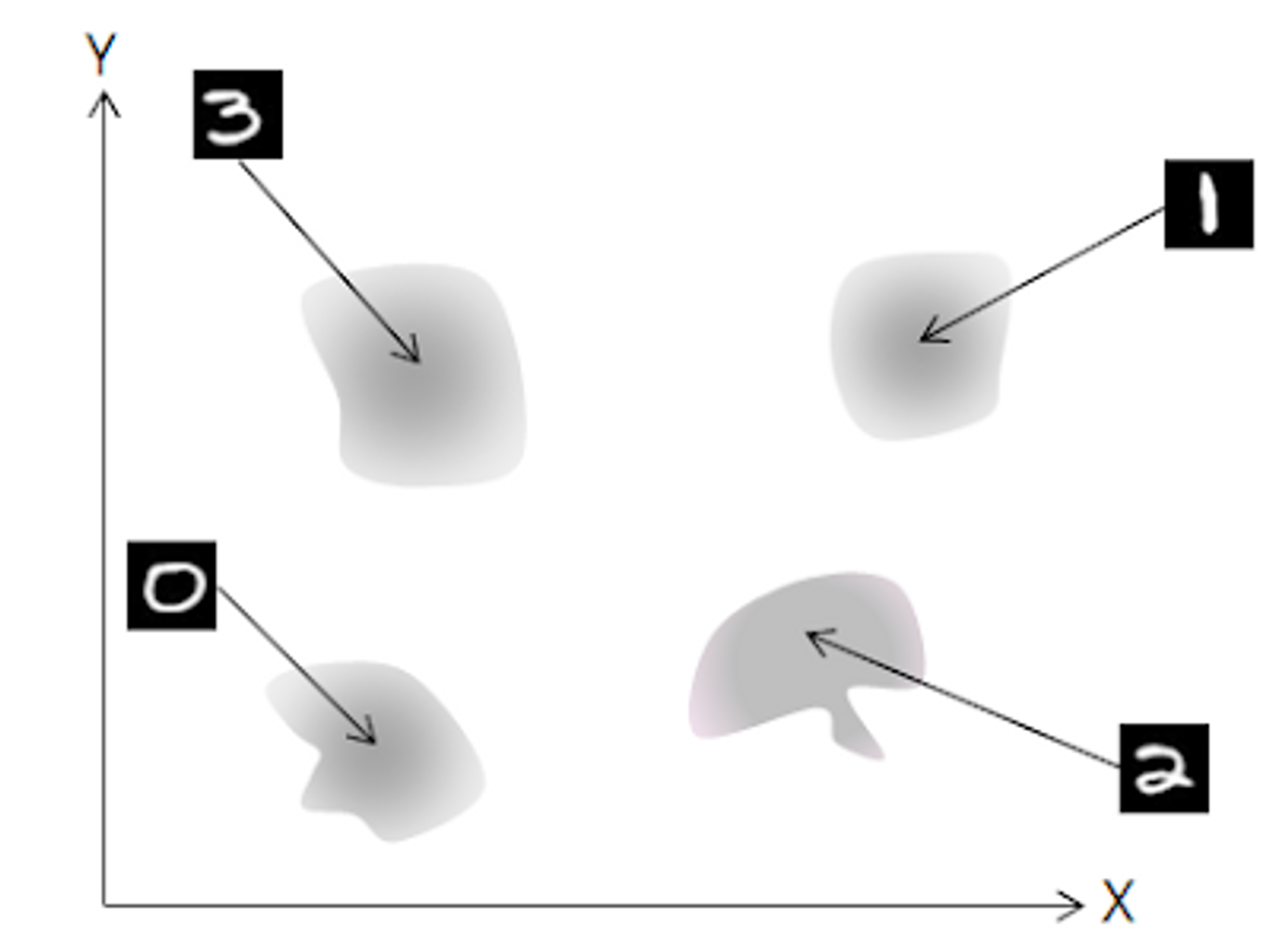
제대로 학습된 분포

Generator가 Discriminator를 속이기 위해 한 숫자만 생성
WGAN의 단점
- 학습 속도가 느림
- gradient clipping
- 추후 WGAN-GP으로 개선

Different Distances
확률분포 측정 측도 4가지
Pr : real data distribution
Pg : generated data distribution
- The Total Variation (TV) distance

- The Kullback-Leibler (KL) divergence

The Jensen-Shannon (JS) divergence

The Earth-Mover (EM) distance or Wasserstein-1
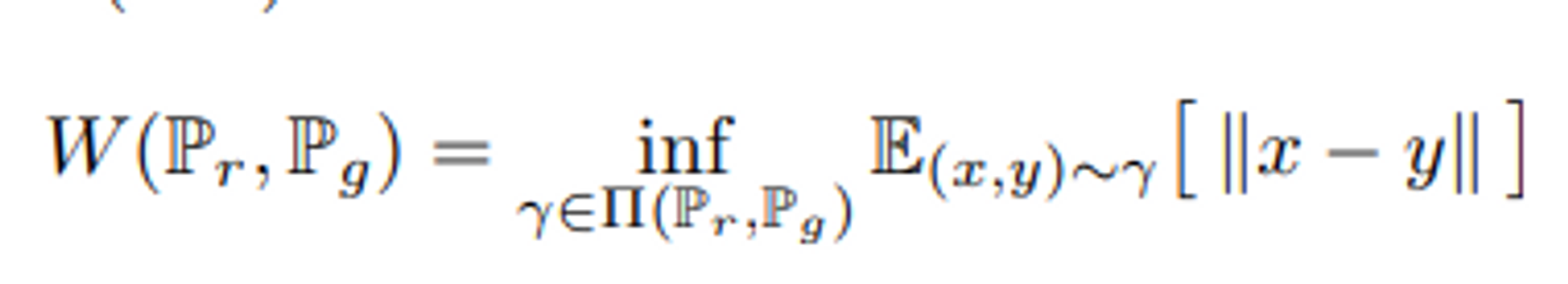
- 파란색 원이 X의 분포
- 빨간색 원이 Y의 분포
- 𝛘가 결합 확률 분포
- 초록색 선의 길이가 ||x-y||

X와 Y의 결합확률 분포 X에서, 초록색 선 길이들의 기댓값을 가장 작게 추정한 값

In this paper..
- Earth Mover Distance (Wasserstein-1)의 소개와 다른 metric(distance)와의 비교
- EM Distance를 GAN에 적용한 WGAN을 제안하고 WGAN이 EM distance를 estimate할 수 있고, minimize할 수 있음을 보임.
- EM Distance를 사용하면 mode collapsing이 없는지를 이론과 실험으로 증명
EM distance의 타당성

Total Variance(TV) Distance : 두 확률 분포의 측정값이 벌어질 수 있는 가장 큰 값을 뜻함.
: 아래그림에서 빨간색 A의 영역 안에 있는 A들을 대입하였을 때, Pr(A)와 Pg(A)의 값의 차 중 가장 큰 것을 뜻하게 되며 , 만약 두 확률분포의 확률밀도함수가 서로 겹치지 않는다면 TV Distance는 1을 나타냄.

- KL Divergence : 분포들이 겹치지 않을 경우에 KL이 발산하여 무한대값을 나타냄

- Jensen-Shannon Divergence(JSD) : 분포들이 겹치지 않을 경우 발산하지는 않지만 상수인 log2로 고정되어버려 "얼마나 먼지"에 대한 정보를 줄 수가 없음 (상수값이므로 미분시 0 → 역전파를 통한 업데이트 x)

결론적으로 위에서 나왔던 Distance들은 두 분포가 서로 겹쳐지는 경우에는 0, 겹치지 않는 경우에는 무한대 또는 상수로 극단적인 거리 값을 나타내게 됨. 이는 discriminator와 generator가 분포를 학습할 때 위 세가지 distance를 기반으로 학습하게 된다면 학습에 어려움이 많다 라는 것을 의미함.
반면 EM Distance의 경우 분포가 겹치거나 겹치지 않는 경우에도 θ를 유지하기 때문에, 학습에 사용하기 쉽다!!
함수가 continuous해야 수렴이 안정적이기 때문에 이러한 방법을 고안해낸 것!!
EM Distance

- γ : 를 Pr, Pg간의 joint distribution 중 하나 (= coupling)
- Π(Pr, Pg) : marginal이 Pr, Pg인 모든 joint distribution들의 집합
- 기존의 분포를 다른 분포로 이동할 때 옮겨야 하는 질량의 크기를 나타내는 Distance ; 거리의 기대값에 infimum(두 분포의 joint distribution space에서 계산됨)
- w를 하나 샘플링하면 X(w)와 Y(w)를 뽑을 수 있게 됨. 이 때 두 점 간의 거리 d(X(w),Y(w)) 역시 계산할 수 있음 :)





- z샘플링을 계속 할수록 (X,Y)의 joint distribution γ 의 윤곽이 드러남
- 더불어서 (P,Q)는 γ의 marginal distribution이 됨.
- 이 때 γ가 두 확률변수 X,Y의 연관성을 어떻게 측정하느냐에 따라 d(X,Y)의 분포가 달라지게 됨.
- P와 Q는 바뀌지 않기 때문에 X와 Y가 분포하는 모양은 변하지 않음. 다만 w에 따라 뽑히는 경향만 달라짐.
- Wasserstein distance는 이렇게 여러가지 γ중에서 d(X,Y)의 기대값이 가장 작게 나오는 확률분포를 취하게 됨.

블록을 움직이는 일의 방법들을 joint probability distribution으로 생각할 수 있음.
EM distance를 사용하기 위한 제약조건

- Pr : 학습하고자 하는 목표 distribution
- Pθ : 학습시키고 있는 현재의 distribution
- z : latent variable의 space
- 함수 g는 latent variable z를 x로 mapping하는 함수
- 이 때 gθ(z)의 distribution이 Pθ가 된다.
- g가 θ에 대해 연속한다면, Pr와 Pθ의 EM distance 또한 연속한다.
- g가 Lipschitz조건을 만족한다면, Pr와 Pθ의 EM distance 또한 연속한다.
Wasserstein GAN

- Pr과 Pg의 joint distribution을 계산할 수 없음(Pr이 우리가 알고자 하는 대상)
- Kantorovich-Rubinstein duality을 이용해 다음처럼 식을 변형
- parameter가 추가된 f 로 수식을 바꾸고, P_θ를 g_(θ)에 대한 식으로 바꾸면 아래와 같은 수식이 된다. ( f_w는 Discriminator라고 이해하면 쉬움!)
관련자료 : Kantorovich-Rubinstein Duality
Jupyter Notebook Viewer
$D_{i,j}\geq f(x_i)+g(x_j) =f(x_i)-f(x_j)$ $D_{i,j}=D_{j,i}\geq f(x_j)-f(x_i)$ $\Rightarrow |f(x_i)-f(x_j)| \leq D_{i,j}=||x_i-x_j||$
nbviewer.org

즉 f(x)는 Lipschitz조건을 만족하는 함수로, dscriminator역할을 하는 함수!!
critic의 loss function 항 자체가 EM distance를 의미하므로, 위 loss function을 최대화(최대화 이유 : Kantorovich-Rubinstein duality를 통해 supremum으로 변형됨, 이후 parameter 식으로 변형하면서 maximize로 바뀌게 됨)하는 함수 f를 찾는 문제가 됨. 여기서 w는 함수 f의 parameter, 즉 critic의 parameter이며, maximize이므로 w에 대한 gradient ascent.

generator의 loss function 역시 Theorem3에서 정의한 대로, 변형된 Wasserstein distance 식을 θ에 대해 미분하여 앞의 식을 사라지게 하면 얻을 수 있고 generator의 경우, Theorem3에서 미분 결과에서 볼수 있듯이 앞에 -가 붙어있기 때문에 θ에 대한 gradient descent가 됨!!


n_{critic}번 만큼 critic을 학습시키고 Pr과 P(z)(P_θ 역할)를 미니배치만큼 샘플링한 후에, critic의 loss function을 이용하여 parameter w를 update 시킴.
여기서 update 후 clip(w, -c, c) 라는 부분은 Lipschitz조건을 만족하도록 parameter w가 [-c, c]공간에 안쪽에 존재하도록 강제하는 규제를 걸어줌 → 이를 Weight clipping이라고 함!
Weight clipping 방법을 통해 반드시 Lipschitz조건을 만족하게 되는 것은 아니며, 휴리스틱한 방법으로 설명하고 있고 논문 저자 또한 이러한 방법은 안좋은(?) 방법이라고 설명하고 있음. (후속 연구에서 해결해주길 바람.. → SNGAN)
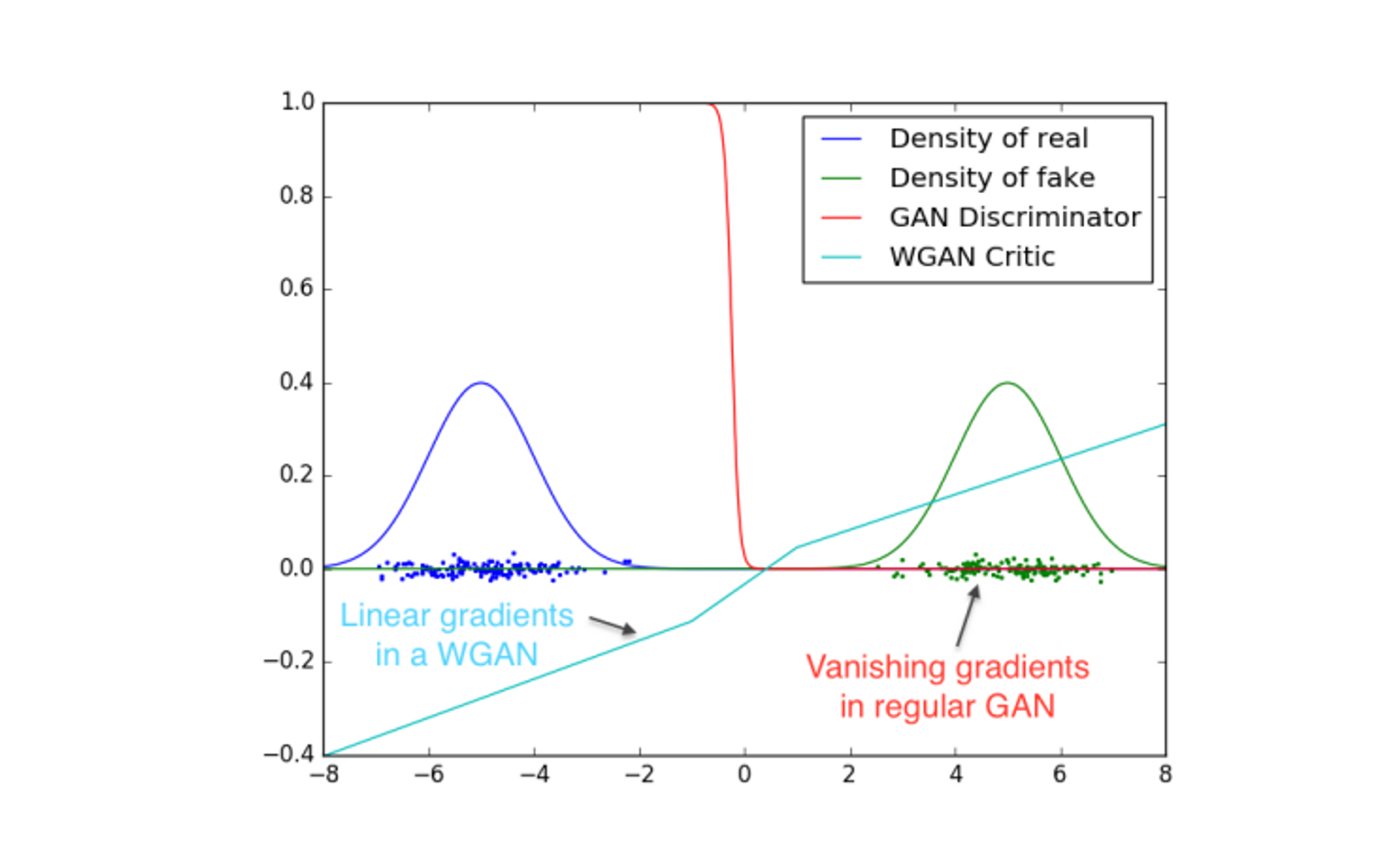
두 가지 Gaussian distribution에서 샘플링을 진행했고, 일반적인 GAN Discriminator를 사용했을 때 학습된 Discriminator가 step function 모양으로 학습이 됨을 실험으로 확인하였고, WGAN Critic을 사용하게 되면 L1 Lipschitz contion에 의하여 smooth한 모양으로 학습이 진행됨을 확인할 수 있었으며, 결과적으로 mode collapsing 문제를 해결할 수 있었음
Empirical Result

loss가 image Quality에 영향에 대한 실험
오른쪽 JS Divergence사용할때 이미지의 Quality는 조금씩 좋아짐을 확인할 수 있으나 loss는 수렴해버리는 결과를 나타내게 됨. 반면에 WGAN loss를 활용할 경우 이미지 Quality가 좋아질수록 loss도 같이 감소함을 확인할 수 있음.
또한 이미지 Quality가 좋아지지 않는 경우에 대해서도 loss값이 떨어지지 않음을 확인함.

실험을 통해 WGAN을 활용했을 때는 mode collapse 현상이 일어나지 않았고, discriminator와 critic 사이의 balance를 신경쓰지 않고 학습을 진행해도 된다고 함.
Reference
[논문 읽기] Wasserstein GAN (tistory.com)
Learn.AI: [GAN] GAN이 풀어야 할 과제들 (dl-ai.blogspot.com)
Wasserstein GAN 수학 이해하기 I (slideshare.net)



