On the journey of
[CSE URP] GAN(Generative Adversarial Networks) 논문읽기 본문
[CSE URP] GAN(Generative Adversarial Networks) 논문읽기
dlrpskdi 2023. 8. 26. 16:47GAN Original Paper ) https://arxiv.org/abs/1406.2661
Generative Adversarial Networks
We propose a new framework for estimating generative models via an adversarial process, in which we simultaneously train two models: a generative model G that captures the data distribution, and a discriminative model D that estimates the probability that
arxiv.org
꽤나 클래식한 논문이다. Cite 횟수도 4만 여 건 이상인 획기적이면서도 생성모델의 원조(ㅎ) 쯤 되는 그런... 논문.
* https://github.com/nightrome/really-awesome-gan (참고)
GitHub - nightrome/really-awesome-gan: A list of papers on Generative Adversarial (Neural) Networks
A list of papers on Generative Adversarial (Neural) Networks - GitHub - nightrome/really-awesome-gan: A list of papers on Generative Adversarial (Neural) Networks
github.com
Overview

: 노란색 테두리 안의 그림들이 생성된 결과 이미지이다.
Introduction
Deep generative model들은 maximum likelihood estimation과 관련된 전략들에서 발생하는 많은 확률 연산들을 근사하는 데 발생하는 어려움과 generative context에서는 앞서 모델 사용의 큰 성공을 이끌었던 선형 활성화 함수들의 이점들을 가져오는 것의 어려움이 있었기 때문에 큰 영향을 주진 못함. 이 논문에서 소개될 새로운 generative model은 이러한 어려움을 극복해냄.
- Generative model G : Discriminative model이 구별할 수 없도록 training data의 분포를 모사
- Discriminative model D : sample 데이터가 G로부터 나온 데이터가 아닌 실제 training data로부터 나온 데이터일 확률을 추정

- D의 입장에서는 data로부터 뽑은 sample x는 D(x) = 1이 되고, G에 임의의 noise distribution으로부터 뽑은 input z를 통해 생성된 sample에 대해서는 D(G(z))=0 이 되도록 한다. 즉 D는 실수할 확률을 낮추기위해 노력하고 반대로 G는 D가 실수할 확률을 높이기 위해 노력하는데, 본 논문에서는 이를 “minimax two-player game”이라고 표현
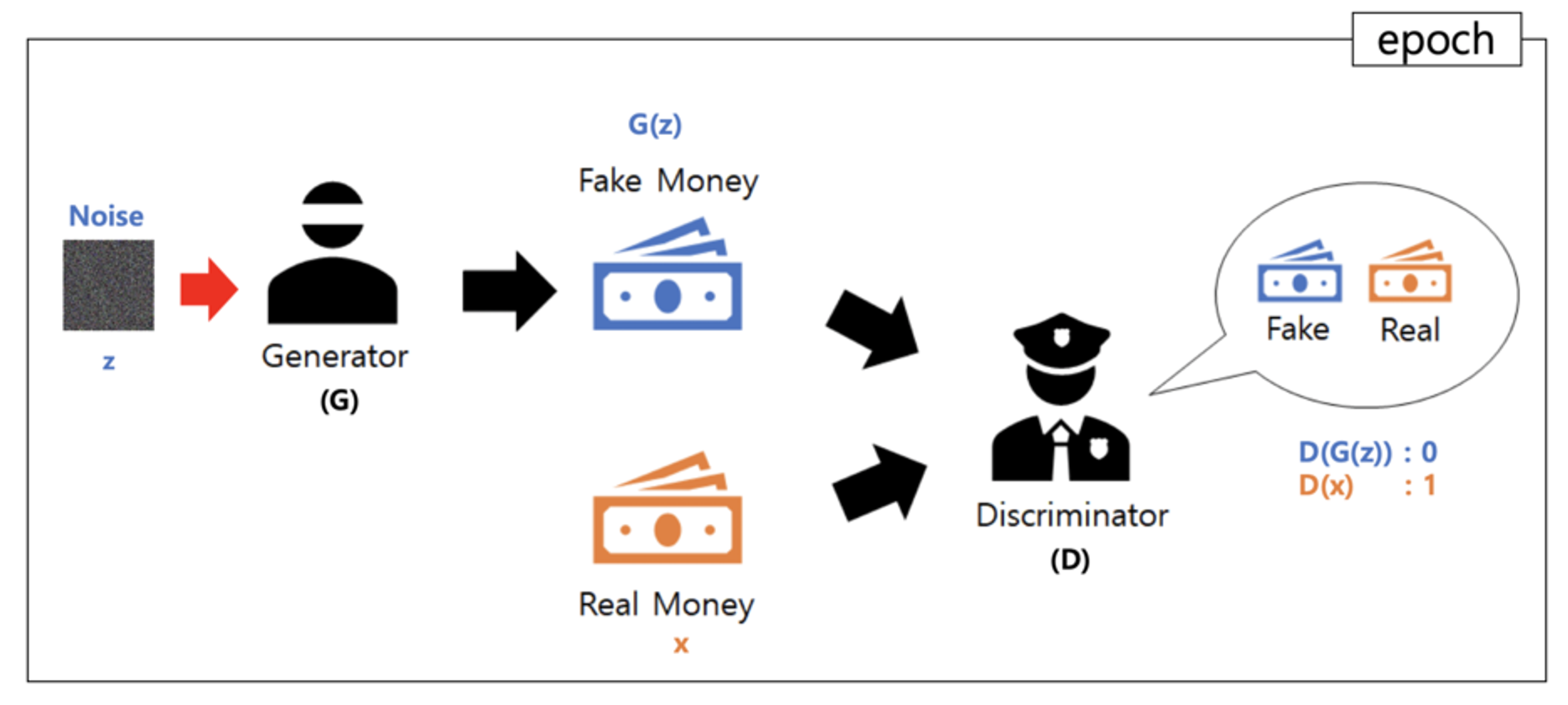
→ GAN의 핵심 컨셉은 각각의 역할을 가진 두 모델을 통해 적대적 학습(=경쟁)을 하면서 ‘진짜같은 가짜’를 생성해내는 능력을 키워주는 것!
Adversarial nets
논문에서는 G와 D모델을 MLP를 활용해 구성하였다.
Generator’s distribution p_g over data $x$를 학습하기 위해 generator의 input으로 들어갈 noise variables p_z(z)에 대한 prior를 정의하고 data space의 맵핑을 G(z;θg)라 표현할 수 있다. 여기서 G는 미분 가능한 함수로써 θg를 파라미터로 갖는 MLP.
한편, Discriminator 역시 MLP으로 D(x;θd) 로 나타내며 output은 확률이기 때문에 single scalar 값으로 나타남. D(x)는 x가 p_g가 아닌 data distribution으로부터 왔을 확률을 나타내게 된다.
이를 수식으로 정리하면 다음과 같다.

- E_x~p_data(x)[logD(x)] : training data x를 D에 넣었을 때 나오는 결과를 log 취했을 때 얻는 기댓값
- E_z~p_z(z)[log(1-D(G(z)))] : noise distribution z를 G에 넣었을 때 나오는 결과를 D에 넣고 그 결과를 log(1-output) 했을 때 얻는 기댓값
- P_x~P_data(x) : G와 D에 들어가는 input이 무엇을 바탕으로 나왔는지 알려주는 표기. 즉 x가 p_data(x) → x는 training data에서 나온 분포라는 것을 의미
이 방정식을 D의 입장, G의 입장에서 각각 이해해본다면

→ 따라서 D의 입장에서 value function V(D,G)의 이상적인 최대값은 0 이고 G의 입장에서 V(D,G)의 이상적인 최소값은 -∞ 임.

GAN은 discriminative distribution을 동시에 업데이트 하면서 학습하게 됩니다. 따라서 D는 sample distribution에서 비롯된 sample을 generative distribution으로 나온 sample로부터 판별하도록 학습합니다. 그림에서 $x, z$는 각각의 domain을 의미
→ 이 과정을 통해 진짜 이미지와 가짜 이미지를 구별할 수 없을 만한 데이터를 G가 생성해내는 것
Theoretical Results




아래를 k번 반복 (논문에서 k = 1로 실험)
- m개의 노이즈 샘플을 pg(z)로부터 샘플링
- m개의 실제 데이터샘플을 pdata(x)로부터 샘플링
- V(G,D)식 전체를 최대화하도록 discriminator 파라미터 업데이트
이후
- m개의 노이즈 샘플을 pg(z)로부터 샘플링
- V(G, D)에서 log(1-D(G(z)))를 최소화 하도록 generator 파라미터 업데이트
Global Optimality of pg=pdata
어떤 G에서 optimal한 D가 존재한다고 생각한다면, G가 고정된 상태에서 optimal한 D는 다음과 같다.

증명
D와 G를 학습시키는 criterion은 다음을 최대화 하는 것인데,

위의 식을 D(x)에 대해 편미분하고 결과값을 0이라고 두면 optimal한 D는 아래와 같이 얻어짐.


이렇게 얻은 optimal D를 원래의 목적함수 식에 대입하여 생성기 G에 대한 Virtual Training Criterion C(G)를 다음과 같이 유도할 수 있다.

위의 C(G)는 generator가 최소화하고자 하는 기준이 되며, 이것의 global minimum은 오직 p_g = p_{data} 일때 달성된다. 그 점에서의 C(G)값은 log4가 된다.
Cross entropy 교차엔트로피
정보 엔트로피는 하나의 확률분포가 갖는 불확실성(놀람의 정도) 혹은 정보량을 정량적으로 계산할 수 있도록 하는 개념이다.교차 엔트로피는 두 가지 확률 분포가 얼마나 비슷한지를 수리적으로 나타내는 개념이다.
Convergence of Algorithm 1
G와 D가 충분한 capacity를 가지며, algorithm 1의 각 스텝에서 discriminator가 주어진 G에 대해 최적점에 도달하는게 가능함과 동시에 pg가 위에서 제시한 criterion을 향상시키도록 업데이트 되는 한, pg는 pdata에 수렴한다.

- Convex : 아래로 볼록
- Concave : 위로 볼록
- sup : supremum , 상한
추가 증명
G는 objective function을 최소화, D는 최대화시키며 각 네트워크를 학습시킨다는 것은 알겠는데, 서로 적대적으로 최대/최소화를 하며 optimal point에 도달할 수 있을까?
→ 답은 이미 나와 있다. 실제로 generator sample의 distribution과 real data distribution 사이의 간격을 최소화시켜서 0에 가깝게 만들기 때문에!!
즉, pg = pdata에 대한 global optimum을 가진다. → 이걸 objective function을 통해 증명해보자.

- Global optimum이 두 distribution(pg, pdata)가 같을 때임을 증명하기 위한 첫 번째 명제는, 최적화된, 즉 학습이 완료된 discriminator의 값이 위 명제와 같다는 것이다. (minmax에서 안쪽 maxD 먼저 계산해야함)
- 확률분포의 기댓값→적분 공식에 따라서 식은 적분 형태로 첫 번째 line과 같이 쓰일 수 있고, 두 번째 항 dz를 z→x space로 매핑하면 두 번째 line과 같이 g(z)→x, pz(z)→pg(x), dz→dx로 변환된다.
- 두 번째 line은 파란 박스 안의 식과 같은 형태를 가지는데, 저런 꼴의 식은 a/a+b에서 최대값을 가진다. (E.g. 참고)
- 따라서!!!!!! a=pdata, b=pg를 적용해보면, V를 최대화시키는 D는 위 명제와 같다는 것을 알 수 있고, 명제가 증명되었다.

D의 max값을 찾아서 이제 변수가 아니기 때문에 max=C(G)로 두고(새로운 함수. D 빠짐) 식을 다시 정리하면 위와 같다. 단순하게 구한 D를 대입한 결과이다.
- 여기까지 minmax 안쪽의 max를 계산했다. 이제 min을 계산해보자! 즉, min(C(G))를 찾아보자!

두 번째 명제는 pg=pdata인 경우에 C(G)가 global minimum을 가진다는 것이다. 즉, 우리가 원하는, 직관적으로 생각하는 이상적인 결과(pg=pdata)가 수식적으로도 global optimum이라는 것을 증명하는 것이다.
- 일단, 그냥 바로 pg=pdata를 앞에서 구한 D 식에 대입하면 D=1/2가 되겠고, 이어서 C(G)는 -log4의 값을 가진다. 이 -log4가 진짜 최솟값이라는 것을 확인하기 위한 마지막 증명이 다음 슬라이드이다. 끝까지 의심의 끈을 놓지 않는..!!

- line1: 구한 C(G)식을 다시 적고 기댓값을 적분으로 풀어주고, -log4를 빼고 더해준다.
- line2: log4를 log2+log2로 나눠서 분배해준다.
- line3: KL divergence의 식과 JSD의 식에 따라서, 마지막 line과 같이 정리된다.
KL, JSD: 간단히 말해서 두 분포 사이의 거리를 의미한다. 거리이기 때문에 최소값은 0이고, 양수이다.
- 따라서!!! 최종 식 -log4+JSD의 최소값은 -log4+0이고, JSD가 0이기 위해서는 두 분포 사이의 거리가 0인, pdata=pg일 때이다.
⇒ 최종 식 -log4+JSD를 통해서, minmax problem을 차례대로 풀어 global optimum을 찾으면, generator가 만드는 pg이 pdata와 정확히 일치하도록 할 수 있다는 것을 알 수 있다!
⇒ 결국 generator로부터 뽑은 sample을 discriminator가 실제 데이터와 구별할 수 없게 되었다는 것이다. = 우리가 원하는 결과임
'Experiences & Study > CSE URP' 29' 카테고리의 다른 글
| [CSE URP] InfoGAN 논문읽기 (2) Background.2 ~ End (0) | 2023.08.27 |
|---|---|
| [CSE URP] InfoGAN 논문 읽기 (1) Abstract ~ Experiment 1 (0) | 2023.08.27 |
| [CSE URP] Auto-Encoding Variational Bayes (ICLR 2014) (0) | 2023.08.25 |
| [CSE URP] ViT Self-Attention 구조 (0) | 2023.08.25 |
| [CSE URP]BEiT: BERT Pre-Training of Image Transformers (2) (0) | 2023.08.24 |




