230731 PyTorch를 활용한 딥러닝 구현, MCMC, 코드분석

Pt.1 : MLP vs CNN

MLP - 데이터를 1차원 배열로 만들어 가중치를 계산 vs CNN - 데이터를 convolution과 pooling을 반복하여 가중치를 계산

그래서 MLP는 CNN의 하위 개념에 속하며, Convolution과 pooling을 비교해자면 convolution : data에 가중치 filter을 convolution하고 pooling: 최대/최소/중간값 등을 선택하는 filter을 통해 data size을 축소시킨다는 점이 다름. 

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
#import set_matplotlib_korean
from torchvision import datasets, transforms
from matplotlib import pyplot as plt

기본적으로 파이토치를 사용하면 저렇게 array 형식으로 바뀌는 것을 확인할 수 있다

---

Filter로 넘어가보자. 크게 I, F, P, S 4개 변수가 있는데 I = 입력 Feature Map 크기, F = Kernel Size = Filter Size, P = Padding(모서리 채워주는 거. 사이즈를 맞춰야 하니까 말하자면 여백을 넣어주는 거다) , Strides(몇 단위로 이동하니?) 인데 이를 공식화한 게 아래 이미지이다. O = Output! 

---

MCMC(Monte Carlo Markov Chain)

•Monte Carlo : 통계학의 특성상 무한한 시도를 거쳐야지만 진짜 답을 알 수 있지만 현실적으로 불가능하기 때문에 수많은 유한한 시도를 거쳐 정답을 유추해보는 것

•Markov Chain : 어떤 상태는 그 바로 전 상태에 의해서만 영향을 받는다는 것

•Markov Chain Monte Carlo : 첫 샘플을 랜덤하게 선정한 뒤, 그 다음번 샘플은 첫 샘플에 의해 추천이 되는 방식의 시도를 무한히 해본다는 것

그렇다면 MCMC - 샘플링(Sampling)은 어떻게 될까?

정리하자면, 표본을 직접적으로 샘플링할 수 없는 타겟 분포 p(x)에서 표본을 얻을 수 있도록 하는 sampling 방법이 어떻게 되냐는 것. Sampling이란 수학적으로 Inverse CDF를 계산한 다음, Inverse CDF의 output값을 의미하니까. 

입력값 x에 대해 output인 PDF를 구할 수 있어도 그것이 input x를 알 수 있는 것은 아니기 때문에 CDF를 구해서 inverse CDF를 구할 수 있다면 input x값을 알 수 있다는 것.  모든 CDF가 (0, 1)사이의 uniform ditribution을 따르기 때문.얘를 수식화해보자면 아래와 같으며, 출처는 all paper...

 

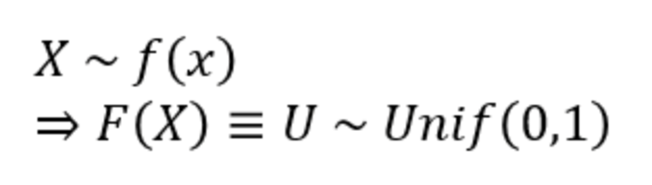
그러나 sampling 상에서, inverse CDF를 계산하는 건 쉽지 않기 때문에 이런 경우 Rejection Sampling을 사용할 수 있다. Input X의 pdf를 알고 있을 때 이 PDF f(x)를 target distribution(타겟분포)라고 하고, proposal distribution g(x)를 별도로 설정하는데 g(x)로는 uniform/ normal distribution 등이 가능하며 최대한 f(x)와 유사한 형태를 띠는 분포가 좋다. 어떤 상수 c에 대해 c * g(x)가 f(x)보다 항상 크거나 같아지면, 이 c*g(x) 를 e(x)라는 새로운 이름의 분포로 불러준다. 

e(x)에서 샘플링을 하고 일부를 무작위로 reject하려고 할 때, rejection ratio는 f(y) / e(y) 혹은 f(y) / (c*g(y)) 로 계산 가능. 알고리즘 순서를 따라가보자. 

g(x)에서 sampling 진행, sample Y 생성

Uniform distribution 에서 sample U 생성

Rejection Ratio 계산

U와 Rejection Ratio 비교, U >= rejection ratio 이면 처음으로 돌아감

U < rejection ratio이면 Y를 X라 하고 target distribution f(x)의 sample로 저장

이 5단계가 정석적인 방법이지만 다른 방법도 있다. 그 방법이 Metropolis - Hasting Method. 한국어로는...메트로폴리스-헤이스팅스 알고리즘이라고 부른다.

 

비교하는 방식은 위 수식과 같다. MH 방법론은 사실 Metropolis 알고리즘의 developed version쯤 되며, 베이지안 접근법을 활용한 연구에서 모수 추론을 위해 가장 널리 사용되는 방법이기도 하다 :) 전반적인 알고리즘의 흐름은 거의 같지만...

---

생성형 모델이 이렇게나...어려운 줄은 몰랐다

재밌긴 한데 정말 어렵다.....나무만 보느라 숲을 보지 못하면서 연결을 못하는 너낌,,,, 더더더더더 공부해야겠다^0^....