[논문읽기] VQ-VAE (Neural Discrete Representation Learning)

Original paper ) https://arxiv.org/abs/1711.00937

Neural Discrete Representation Learning

https://arxiv.org/pdf/1711.00937.pdf (Directly Connected to pdf) ;

쉽게 말해, 이산표현을 학습하는 생성모델이라 할 수 있다. 

---

1. Abstract

• 본 논문에서는 discrete representation을 학습하는 생성모델을 소개한다.
• VQ-VAE(Vector Quantising VAE)와 VAE의 다른점은 다음과 같다.
  • encoder의 출력이 discrete하다.
  • prior가 덜 static하게 학습된다.
• VQ-VAE는 Vector Quantising기법을 사용하였으며, VAE의 posterior collapse 현상을 해결했다.
  • posterior collapse는 autoregressive decoder가 너무 강력하면, latent가 무시되는 현상을 의미한다.
• images, videos, speech에서도 좋은 성능을 보인다.
  • image, video, nl 또한 discrete domain으로 representation이 가능하기 때문

2. Introduction

• 최근 다양한 분야에 대해 발전된 생성 모델들이 제안되았지만, 대체로 불필요한 generic representation이 학습되었다.
• VQ-VAE의 목적은 maximum likelihood를 최적화하는 동안 latent space 상의 중요한 feature들을 유지하는 것이다.

3. VQ-VAE

• VAE는 다음과 같이 구성되어 있다.
  • encoder → input data x, prior distribution p(z)가 주어졌을 때, discrete latent random variable z에 대한 posterior distribution q(z|x)를 파라미터화한 네트워크
  • decoder → p(x|z)
• VAE의 extension은 다음과 같다.
  • autoregressive prior and posterior models
  • normalising flow
  • inverse autoregressive posteriors

3-1. Discrete Latent variables

Equation 1

• discrete latent variables z는 embedding space e에서 nearest neighbour look-up을 통해 계산된다.
  • posterior categorical distribution q(z|x)
    • k는 z_e(x)의 인덱스를 의미한다.
    • encoder output z_e(x)의 k번째 vector와 L2 distance가 최소로 되는 j번째 codebook vector e_j가 존재할 때, 1, 나머지는 0으로 one-hot encoding.
    • q(z|x)는 deterministic하다.

Equation 2

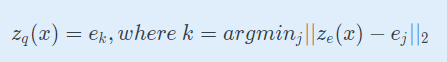
• z_e(x)를 가장 근접한 codebook vector e_k로 대체한 것이다.

3-2. Learning

• Equation 2에는 실질적인 gradient는 존재하지 않는다.
• 그래서, grdient를 decoder input z_q(x)로부터 encoder output z_e(x)에 복사한다.
• forward시, nearest embedding z_q(x)는 decoder로 전달된다.
• backward시, gradient nabla_zL이 encoder로 전달된다.
• encoder의 output representation z_e(x)와 deocder의 input representation z_q(x)는 동일한 D 차원을 공유한다.
  • gradient는 encoder가 reconstruction loss를 낮추기 위해 출력을 어떻게 변해야 할지에 대한 유용한 정보가 포함되어 있다.

Equation 3

• Equation 3는 전반적인 loss function을 의미한다.
• 해당 loss function은 3가지 term으로 구성되어 있다.
• sg : stop gradient
• reconstruction loss ; which optimizes the decoder and the encoder 식은 아래와 같다. 

z_e(x) to z_q(x)로 인해 codebook 벡터 e_i는 위 reconstruction loss로부터 아무 gradient도 전달받지 못한다. 

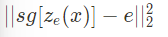
VQ의 objective는 codebook vector e_i를 encoder의 output z_e(x)로 이동하게 한다.

• commitment loss
• embedding space의 크기는 dimensionless하기 때문에, codebook 벡터 e_i는 encoder의 파라미터처럼 빠르게 수렴할 수 없다.
• 고로, encoder와 embedding space와의 수렴 속도를 일치시키기 위해 commitment loss를 도입했다.
• Beta는 commitment loss의 가중치를 의미하며, 0.1부터 2.0까지는 model이 해당 하이퍼 파라미터에 robust했다.
• 본 실험에서는 Beta값으로 0.25를 사용했다.
• 위 설명에서는 codebook vector를 이해를 위해 1D로 설명했지만 실제로는 2D 이상의 형태로 사용한다.
  • ImageNet : 32 * 32
  • CIFAR10 : 8 * 8 * 10

이때 , MLE에 대해 간단히 짚고 가자. 

AE 설명 당시, 생성 모델은 주어진 데이터 x를 잘 설명할 수 있는 방향으로 log likelihood를 maximize해야 한다 했다

→ MLE (Maximum Likelihood Estimation)

 

그렇다면 MAP(Maximum a posteriori estimation)은 뭘까. 아래 bayesian probability로 표현된 식을 보자. 

여기서 MAP 추정 식은 아래와 같다. 

Equation 4

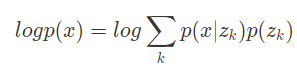
• 사건 A=x
• 모집단 B = z_k
• Equation 4는 VQ-VAE의 log likelihood를 MAP-inference로 나타낸 것이다.

Equation 5

• Jensen’s inequality를 사용하여 VQ-VAE의 log likelihood를 다음과 같이 표현할 수 있다.
  • Jensen’s inequality는 VAE에서 p(z), p(z|x), q_ φ (z|x)간의 관계를 설명하여 ELBO term을 유도할 때 사용했다.
  • Prior distribution p(z) - 간단하게 설정한 분포
  • True posterior distribution p(z|x) - 입력에 대해 주어진 현재의 분포
  • Appriximation clss distribution q_ φ(z|x) - 근사 대상 분포

3-3. Prior

• (discrete latent) prior distribution p(z)는 categorical distribution이다.
• feature map 내의 다른 z에 의해 autoregressive해질 수 있다.
• VQ-VAE를 학습하는 동안, prior는 constant하고, uniform하다.
• 학습 후에는 ancestral sampling을 통해 x를 생성한다.
• discrete latent를 생성하기 위해 본 실험에서 사용한 모델
  • image : PixelCNN
  • raw audio : WaveNet

실험은 다음 포스팅에...