On the journey of
[딥러닝 홀로서기] 4.Binary / Multi-Label Classification 본문
[딥러닝 홀로서기] 4.Binary / Multi-Label Classification
dlrpskdi 2023. 8. 31. 06:42|
Supervised Learning
|
Unsupervised Learning
|
Reinforcement Learning
|
|
|
Discrete
|
Classification
|
Clustering
|
Discrete Action Space Agent
|
|
Continuous
|
Regression
|
Dimensionality Reduction
|
Continuous Action Space Agent
|
Semi - Supervised Learning = Supervised Learning + Unsupervised Learning (준지도학습)
Supervised Learning : 어떤 데이터 x가 있을 때 이것과 라벨링 된 y가 있을 때, 어떤 x는 이 데이터는 어떤 값이다(ex. 이 사진은 고양이 사진이다) 이런 라벨링이 되어 있을 때 이것을 가지고 훈련시킨 것이 Supervised Learning이다.
그리고 그러한 라벨들, output들이 Discrete vs Continuous한가?
Continuous 한 것들은 예를 들어 집값이 서울 중심부에서 떨어진 거리가 x이고 집값이 y일 때 continuous하게 예측을 해야 하는 경우로 이것이 Continuous의 Regression problem이다.
Classification의 경우, 사진이 들어왔을 때 이것이 고양이 사진인가, 개 사진인가 구별하는 것이다.
이러한 Classification problem을 Machine Learning을 통해서 어떻게 풀어볼 것인지가 이번 주제이다.
Example of Binary Classification : Dog or Cat?
Show this facebook feed to user or not?
그 중에서도 Binary Classification이란 것은 Classification해야 할 class가 두 가지인 경우이다.
예를 들어 사진이 개인가, 고양이인가, 또한 facebook의 경우 새로운 뉴스 피드가 떴을 때 이것을 사용자에게 보여줄 것인지 아닌지 등이 있다.
- 0, 1 encoding (원핫인코딩) : 수학적으로 나타내고자 두 경우를 0과 1에 대응시켜 생각해보는 것.
ex) Dog(0), Cat(1) / Show the feed(0) , Do not show the feed(1)
Binary Classification Hypothesis
모든 Machine Learning problem들은 세 가지 키워드로 설명될 수 있다.
- model을 뜻하는 Hypothesis
- 잘 예측하면 할 수록 값이 줄어드는 cost
- cost를 바탕으로 Hypothesis의 parameter를 tuning하는 optimization과정
으로 나눌 수 있다.
그래서 Binary Classification Hypothesis에 대해서 배워볼 것이다.
Pass(1)/Fail(0) based on study hours
Can we use Linear Regression?
x축 : Study Hours
y축 : Pass(1), Fail(0)

또 다른 예시로 input값이 study hours일 때 학생이 pass 할 것인가 fail 할 것인가에 대한 문제이다.
pass한 경우를 1, fail한 경우를 0이라 하자: 학생들의 정보를 통해서 sampling하면, study hour가 적으면 대체적으로 fail, study hour가 어느 정도 높으면 pass할 것.
그러면 이러한 data distribution을 본다면 저번의 linear regression을 써서도 할 수 있지 않을까라는 생각이 들 수 있다.
예를 들어 b가 0이고 W가 적절한 값으로 직선이 그려지고, pass(1) fail(0)을 나타내는 y축에서 0.5보다 큰 값을 가지게 되면 pass, 작은 값을 가지게 되면 fail, 이런 식으로 linear regression을 써도 될 거 같아 보이지만, 실제론 문제가 생긴다.
ex) Study Hours가 50시간을 공부한 학생의 데이터가 들어오면 당연히 pass가 찍힐 것이다. 그러면 50시간인 데이터도 고려해주기 위해 W값이 update되어 새로운 직선이 그어지는데, 이렇게 되면 0.5에 대응되는 Study Hours의 x값이 밀려나면서 실제로 pass한 학생들이 0.5보다 왼쪽(fail 영역)에 있게 되어 fail로 분류되는 경우가 발생한다. 그래서 데이터에 따라서 예측을 잘 할 수 없는 경우가 발생한다.
또 하나는 pass를 1로 정의하고 fail을 0으로 정의했는데, 직선을 그어버리면 continuous한 값이 앞으로 나오기 때문에 1보다 큰 값이 나오거나 0보다 작은 값이 나올 가능성이 있다. 그래서 linear regression hypothesis를 그대로 가져가기에는 문제가 있다.
Logistic Hypothesis
H(x) = Wx + b : Linear Regression Hypothesis를 수식으로 쓴 것
H(x) = G( Wx + b )
Linear Regression Hypothesis 수식을 살짝만 변형하면 Classification에도 사용할 수 있을 것 같은데 어떻게 사용할 지 고민하다가, 적절한 함수 G를 수식에 덮어씌우게 되면 0, 1로 Binary Classification하는 문제에 대해 쓸 수 있을 것 같다는 생각을 하게 된다.
Sigmoid (Logistic) Function
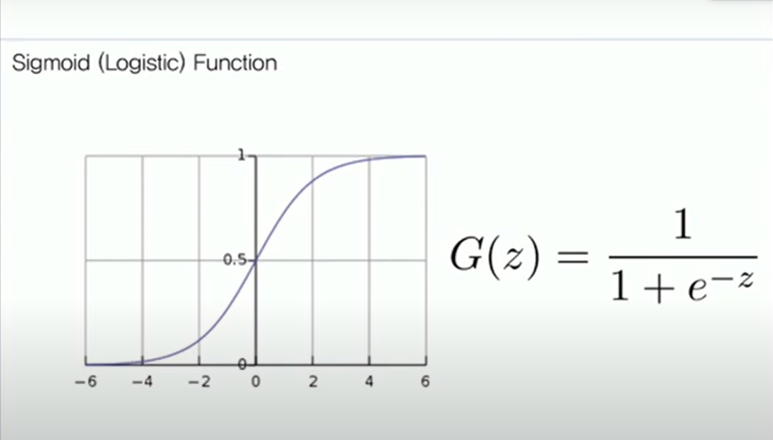
그래서 등장한 것이 Sigmoid Function이다.
Sigmoid Function의 식이 G(z)에 해당하고 그래프는 좌측의 그림이다. 보면 전체 실수값에 대해 0과 1 사이의 값으로 constrain이 되는 것을 볼 수 있는데, G(z)의 z에 양의 무한대를 넣을 경우 1이 되고, 음의 무한대를 넣을 경우 0이 된다.
어떤 실수 값을 넣더라도 0과 1 사이의 값으로 잘 constrain되는 것을 볼 수 있다.
함수의 이름이 Sigmoid 함수인 이유는 그리스 문자 S와 닮아서이며, Logistic Function이라고도 부른다.
Logistic Hypothesis
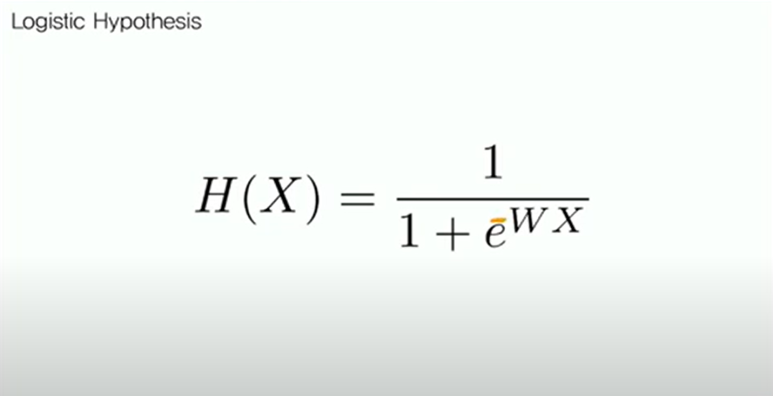
그러면 linear regression hypothesis를 sigmoid function에 넣어 hypothesis가 위와 같이 바뀌는 것을 볼 수 있다.
이것이 Logistic Hypothesis이다.
Binary Classification Cost
새로운 hypothesis를 정의했으면 그에 맞는 새로운 cost function을 정의해야 한다.
Cost Function ; Can we use the cost function of linear regression?
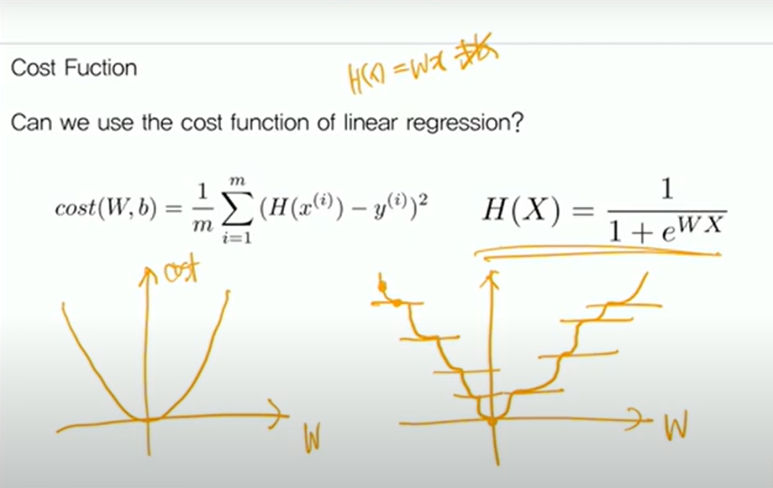
linear regression에서 얼마 바뀌진 않았기 때문에 linear regression에서 썼던 mse cost를 그대로 가져다 쓸 수 있다는 생각을 할 수 있다. 지난 H(x) = Wx( + b는 생략한다)에서 W에 따른 cost에 대한 그래프를 그릴 때 기본 이차함수가 나온 것을 볼 수 있었다. 그런데 hypothesis가 우측과 같이 바뀌었을 때 똑같은 작업을 해보면 구불구불한 이상한 이차함수가 나오는 것을 볼 수 있다.
이러한 cost function(이상한 이차함수)을 쓰면 발생하는 문제가 있는데, 중간중간에 gradient가 0인 점들을 볼 수 있는데, 이 점에 한 번 도착하게 되면 gradient가 0이기 때문에 training을 많이 돌려도 더 이상 step을 밟아나갈 수 없게 된다.
그래서 이러한 local minimun에 갇혀버리게 된다. 때문에 새로운 cost function, hypothesis를 정의해야 한다.
Cross Entropy
Difference between two probability distribution

Cross Entropy라는 개념은 cost function에 필요하다.
화학이나 물리에서 Entropy의 개념은 시스템이 얼마나 불안정한가를 나타내는 지표로 쓰인다.
P(x)는 실제 확률, Q(x)는 예측한 확률이다. 예를 들어 대한민국과 독일이 축구를 할 때의 상황이 binary classification인데(한 쪽이 이기면 다른 쪽은 지므로), 한국이 이길 확률을 계산했을 때 Q(x) = 0.01인데 실제 상황에서 한국이 이겼다면 P(x) = 1이다.
이를 계산하게 되어 식 앞의 마이너스 기호 -를 log로 가져온다면 0으로 다가갈 때 무한대의 값이 나온다. 때문에 P(x) = 1과 - log에서의 무한대의 값을 곱하면 엄청나게 큰 값이 나온다. 불안정성이라는 것은 얼마나 예측을 잘 못했는지와 같은데, 예측에 반해서 놀라운 결과가 나올 수록 커지는 값을 Cross Entropy라 한다.
반대의 경우, 대한민국과 중국이 경기를 하는 상황에서 한국이 이길 확률은 Q(x) = 0.9로 계산하여 예측하였을 때, P(x) = 1일 경우 1과 -log0.9와 곱해지므로 작은 값이 나와 잘 예측한 것으로 볼 수 있다. 따라서 cost function이라는 것은 잘 예측할 수록 적은 값이 나오고 반대의 경우 큰 값이 나오는 것을 볼 수 있고, linear regression에서는 mse loss가 그 역할을 잘 수행해준다. 이러한 개념을 잘 가져다 쓰면 적절한 cost function을 정의해볼 수 있다.
Cost Function
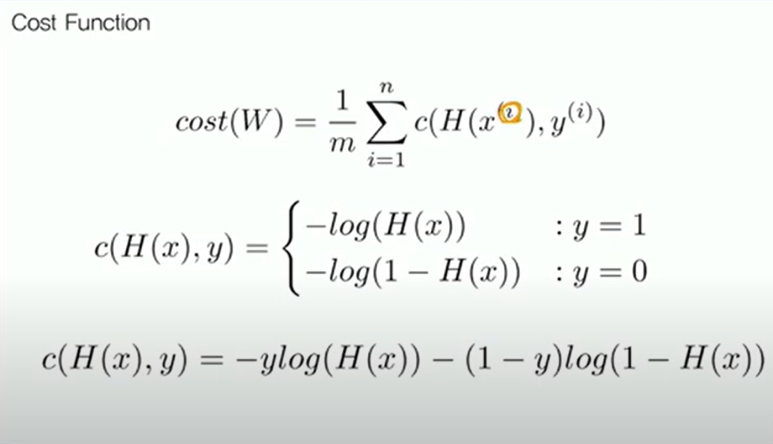
첫 번째 식 cost(W)에서는 i는 n개의 각 데이터 중 i번째 데이터라는 것이고, 각 데이터의 cost를 계산하고 1/m을 하여 평균을 낸 것으로 볼 수 있다. 각 cost를 나타낼 때, mse에서는 거리 사이의 제곱이었는데, 여기서는 두 번째 식 c(H(x), y)와 같이 정의할 수 있다. 세 번째 식은 두 번째 식을 합친 것이다.
시험에 pass/fail하는 경우의 예를 돌아가보자.
y = 1의 경우가 pass, y = 0의 경우가 fail이라 생각할 때, 학생이 pass한다고 예측하여 예측 확률을 1에 가까운 값으로 계산했을 때, 실제로 시험에 pass한다면 y = 1의 경우가 되어 해당 그래프에 값을 넣어보면 cost가 낮게 잘 나온다. 그런데 학생이 fail한다고 예측할 경우, 실제 시험에서 pass를 한다면 y = 1일 경우의 그래프에서 큰 값이 나오는 것을 볼 수 있다. 반대로, 학생이 pass한다고 예측했는데 fail한 경우에는 y = 0일 때의 그래프를 보면 큰 값이 나오고, fail한다고 예측할 때 실제로 fail한 경우에는 y = 0일 때의 그래프에서 작은 값이 나오는 것을 볼 수 있다.
이러한 식으로 cost를 정의한다면 binary classification에서도 잘 쓸 수 있겠다 싶다! 잘 예측하면 값이 작아지고 그렇지 못하면 값이 커지기 때문이다. Binary Classification에서 실제 값이라는 것은 이 클래스인가 다른 클래스인가라는 문제이기 때문에, 이 클래스일 확률이 1이고 다른 클래스일 확률이 0이 되는 상황이다.
Binary Classification에 대한 정리를 하자면, 두 가지의 binary classification은 어떤 두 가지의 input이 들어갔을 때 어느 클래스인지 판별하는 문제였다. 그리고 각 클래스를 0과 1로 대응을 시켜 이러한 문제를 linear regression으로 풀어보려 하면 잘 맞지 않기 때문에 linear regression model에 Sigmoid function을 씌운 새로운 hypothesis를 생각했고, 그에 걸맞는 cross entrophy를 기반으로 한 cost function을 새로 정의하여 Machine Learning problem에 hypothesis와 cost를 정의하였다.
실제로 학습할 때는 똑같이 gradient descent algorithm을 쓸 것이다. 왜냐하면 H(x)가 결국 Wx + b이기 때문에 조금 식이 복잡해지더라도 W와 b에 대해서 편미분을 할 수 있기 때문이다. 편미분이 가능하므로 gradient descent algorithm도 사용 가능하다.
Multinomial Classification
Classification problem이 당연히 Binary Classification인 경우에만 있지는 않을 것이다.
class가 여러 가지인 경우도 있을 것인데, 예를 들어 사진이 주어졌을 때 개인지 고양이인지 사람인지 책상인지 등 엄청나게 많은 class로 분류해야 할 경우가 있을 것이다. 이러한 경우를 Multinominal Classification Problem이라고 한다.
이에 대해 배우기 전에 Binary Classification을 좀더 공부해보자.
Binary Classification

아까는 study hour라는 input 하나를 가지고 classification하는 경우였는데, 예를 들어 x1은 study hour로 두고 x2는 attendance로 두 가지 input을 두었을 때, 두 가지 data를 받아 학생이 A, B, C 중 어떤 grade를 받을 지 예측하는 problem을 생각해보자.
그러면 study hour과 attendance 모두 높은 학생이 A를 받을 것이고, 둘 중 하나를 잘 하는 학생은 B를 받고, 둘 다 못한 학생은 C를 받을 것이다. 그럼 아까 Binary Classification의 hypothesis를 다시 가져와보면, Sigmoid(Wx + b)와 같은 형태였다. 그리고 이것이 0과 1 사이의 값이기 때문에 0.5보다 크면 1, 작으면 0이라고 생각할 수 있다.
결국 Sigmoid는 일대일대응되는 증가함수인데, Sigmoid(Wx + b) = 0.5인 경우는 Wx + b가 0일 때이다. input이 x1, x2로 하나보다 많으므로 행렬식이 된 Wx + b를 풀어서 써보면, w1x1 + w2x2 + b이고 이 값이 0이 되어야 한다.
이 식을 보면 직선의 식임을 알 수 있다.
결국 Binary Classification problem은 데이터 포인트들이 평면에 찍혀있을 때(여기서는 input의 개수가 두 개이므로 평면이지만, input의 개수가 늘어날수록 차원이 높아지게 된다) , 2차원에서는 decision boundary 선을 긋는 문제로 생각해볼 수 있다.
Multinomial Classification
그러면 Binary Classification에 대해서는 이러한 모델이 잘 working 했다. 그런데 Multinomial로 넘어오게 되면 한 개의 선을 어떻게 긋더라도 세 개의 영역으로 나누어지지 않는다. 때문에 또 다른 hypothesis를 만들어야겠다는 생각이 들게 된다.
H(X) = XW + b
그러면 새로운 hypothesis를 정의해보자.
아까 Binary Classification에서 hypothesis를 설명할 때, linear regression 모델은 위와 같이 생겼다. 여기에 아래처럼,
H(X) = G(XW + b)
함수 하나를 잘 씌워서 Binary Classification에 이용할 수 있겠다는 생각을 하게 된다. 같은 방식으로 함수를 잘 씌우면 Multinomial Classification에도 이용할 수 있겠다는 생각이 들게 된다.

이것이 Binary Classification에 사용하는 것이었는데, 이를 여러 번 해보자.
class가 여러 개이므로 class마다 continuous한 값을 뽑는다.

위와 같은 linear regression model을 통해 y1, y2, y3가 나온다고 해보자.
y1, y2, y3는 음의 무한대부터 양의 무한대까지 모든 값을 가질 수 있는 continuous한 값이다.
이 y값들이 특정한 함수 G를 잘 거쳐서 각각의 class에 대응될 확률이 나오게 하는 것이 목적이다.
확률의 특성은 그 값이 0과 1 사이의 값이어야 하고, 모든 class에 대응될 확률을 합하게 되면 1이 나와야 한다.
이러한 함수 G를 잘 정의하면 Multinomial Classification에 잘 쓸 수 있을 것이다.
Softmax function
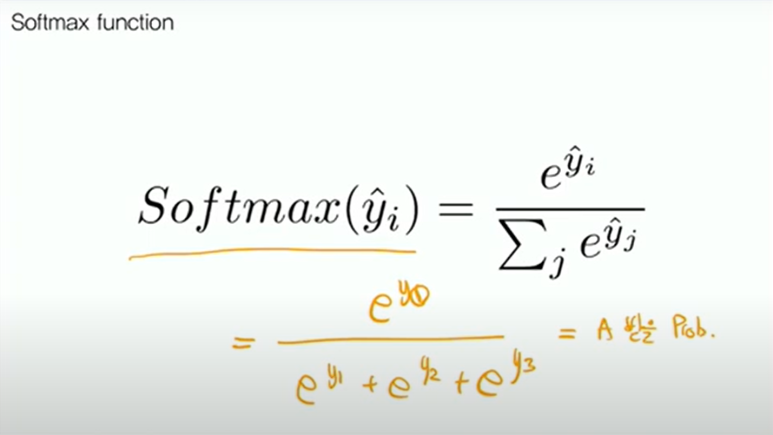
그래서 사람들이 위와 같은 Softmax function이라는 것을 생각해낸다.
이것을 아까 A, B, C 세 가지 class로 나누는 경우에 대입해 보자.
exponential 함수는 항상 양수이기 때문에 분모가 분자보다 항상 클 것이라는 것을 알 수 있어 각각의 값이 0과 1사이의 값으로 나온다. 세 가지 값을 합하면 분모와 분자가 같아지기 때문에 전체 값의 합이 1이 된다.
이러한 함수를 어떤 continuous한 값을 Softmax라는 함수를 거치게 되면, 각각의 class에 대응될 확률로 표현할 수 있다.
여기까지가 Hypothesis에 대한 내용이고, Hypothesis에서 input을 받아 식에서 잘 곱하여 나온 값들이 각각의 class에 대응될 확률들이라고 할 수 있다.
Multinomial Classification Cost
이제 cost를 정의해보자.

Cost function: 예측한 값과 실제 값을 비교해서 나온 값이다.
Softmax 함수를 거쳐 나온, 예측한 확률 값들이 S(y), pred_y라고 하자. 그러면 실제 값 y, true_y는 그 일이 벌어졌는지 아닌지에 따라 1과 0으로 나온다. 이 pred_y와 true_y 사이의 값들을 잘 정의해보자.
아까 Cross Entrophy 개념은 p(x)가 실제 확률이고 q(x)가 예측한 확률일 때, 두 확률 분포가 얼마나 다른지를 보여주는 값이었다. 많이 다르면 예측을 잘 못한 것이므로 불안정해서 값이 높고, 잘 예측한 상황에서는 불안정성이 낮아서 값이 낮았다. 이 Cross Entrophy 개념을 Cost function에 적용해볼 것이다.
이것을 Binary Classification 때와 같이 확률로써 문제를 풀어 나갈 것이므로, Cross Entrophy의 값을 binary 상황에서는 두 개밖에 없으므로 식으로 표현할 수 없었는데, 현재 상황은 이보다 많으므로 sum으로 표현하여 나온 수식이다.
즉 log 안의 값이 Sigmoid(WX + b)에서 Softmax인 S()로 바뀐 것에 불과하다고 Cost function을 정의할 수 있다.
Binary and Multinomial Classification

마지막으로 정리하면, Classification은 크게 Binary와 Multinomial로 분류할 수 있다.
Binary는 분류할 클래스가 두 가지인 경우, Multinomial은 그보다 많은 경우이다.
Binary에서는 모든 실수 값을 0과 1사이로 만들어주기 위해 linear 함수를 Sigmoid(시그모이드)로 씌우면 되고, Multinomial의 경우는 확률을 표현하는 0과 1사이의 값과, 나온 확률을 모두 합하면 값이 1이 되도록 Softmax 함수를 씌웠다.
Cost function의 경우는 둘 다 Cross Entrophy 개념을 빌려와서 쓴 것인데, Binary의 경우는 case가 두 가지밖에 없으므로 식 하나로 표현할 수 있었고 Multinomial의 경우에는 case가 여러 가지이므로 각각의 class에 대해 시그마를 이용하여 구현하였다.
'Experiences & Study > 딥러닝 홀로서기' 카테고리의 다른 글
| [딥러닝 홀로서기] Standalone DL; Regression with Pytorch (0) | 2023.09.05 |
|---|---|
| [딥러닝 홀로서기] 3. Linear Regression (0) | 2023.08.27 |
| [딥러닝 홀로서기] 2. ML Basic (Eng - Kor) (0) | 2023.08.26 |


