[딥러닝 홀로서기] 3. Linear Regression
* 본 포스팅에 포함된 강의안 캡처 및 내용의 저작권은 모두 아래 링크(강의) 에 있음을 밝힙니다.
Original Lec. https://www.youtube.com/watch?v=DWdtr_IURkU&list=PLSAJwo7mw8jn8iaXwT4MqLbZnS-LJwnBd&index=2
Linear Regression : 선형회귀.
독립변수 X와 종속변수 Y가 있을 때 두 변수 간 상관관계와 영향을 파악하는 것도 있지만, 둘 다 1차원 벡터라 하면 x --> y로 가는 함수를 만드는 것이 목표
(Linear) Hypothesis
f(x) = wx + b 의 꼴로 잡아놓았을 때, 다양한 f(x)가 존재할 수 있는데 각각의 f를 hypothesis, 가설이라고 부른다
데이터 분포를 설명하는 가정, 가설이 f이며, 데이터를 가장 잘 표현하는 hypothesis를 찾는 것이 목표이다.
H(x) = Wx + b (f(x) 대신 H(x)로) ; Which hypothesis is better?
w와 b가 고정돼있지 않으므로 여러 개의 그래프를 그려볼 수 있을 것.
그어본 선과 실제 데이터 사이의 거리를 계산하여 좋은지 나쁜지 판단해보면 어떨까라는 아이디어에 착안한 개념이 Cost function이다. 그럼 Cost Function은 뭐 하는 개념일까.
Cost function
Cost function( = Loss function과 같은 개념이다)은 가설의 좋고 나쁨을 정량화할 수 있는 지표이다
- How fit the line to our (training) data
c1 = H(x) - y, H(x) = Wx + b
첫 번째 data point에 대한 cost 정의
data model이 예측한 y(H(x))와 실제 데이터의 y값(y) 사이의 거리를 cost(c1)로 잡는다
BUT 실제로 regression을 할 때 바로 넣지 않는 이유가 음수인 cost 값과 양수인 cost값이 더해져서 0이 돼버릴 가능성이 있기 때문. 예를 들어 두 점 사이의 중간 지점을 정확히 지나가면 양수와 음수 cost를 합하면 0이 나와버린다
cost function이 작다는 것은 model이 잘 표현된다고 하는 상황인데 이렇게 값을 취해버리면 잘 표현되지 않는 model임에도 불구하고 잘 표현된다고 잘못된 판단이 내려질 수 있기에 실제로는 절대값이나 제곱을 취해서 양수로 만들어버린다

ci : i번째 data에 대한 cost 비용
hypothesis에 대한 cost를 정의할 때는 가지고 있는 데이터들을 모두 넣는다(위 사진의 분자에 해당)
m : data point의 개수
H(x) = Wx + b에서 W와 b를 바꿔보며 다양한 시도를 해봤을 때 자신이 한 시도가 좋은지 나쁜지 정량적으로 비교할 수 있는 상황이 됐다

cost는 hypothesis를 input으로 받는 것이다
즉, cost의 input은 W와 b이다
x는 이미 갖고 있는 데이터인데 비해 H는 w와 b에 의해 cost function의 값이 바뀐다
Goal : Minimize cost
minimize cost(W, b)
결국 linear regression에서 학습을 시킨다는 것은 W, b에 의해 결정되는 cost 값을 minimize하는 W와 b를 찾는 것이다
정리
- Hypothesis : 함수의 꼴, parameter가 아직 결정되지 않은 model
해당 model이 얼마나 좋은지 나쁜지 정량적으로 파악하기 위해서 cost function(또는 loss function)이라는 개념을 대입한다
Regression 상황에서 쓸 수 있는 cost function(제곱, 절대값, ...)에 대해서 알아본 것이다
How to minimize cost
Hypothesis and Cost

Simplified hypothesis

보다 간단하게 표현된 수식이다
H(x) = Wx이라고 표현함으로써 (0, 0)을 지나는 간단한 simple line으로 regression을 하는 상황이라고 가정함에 따라 cost function도 W로 보다 간단히 표현될 수 있다



W를 바꿔가며 cost를 찾아낼 수 있다
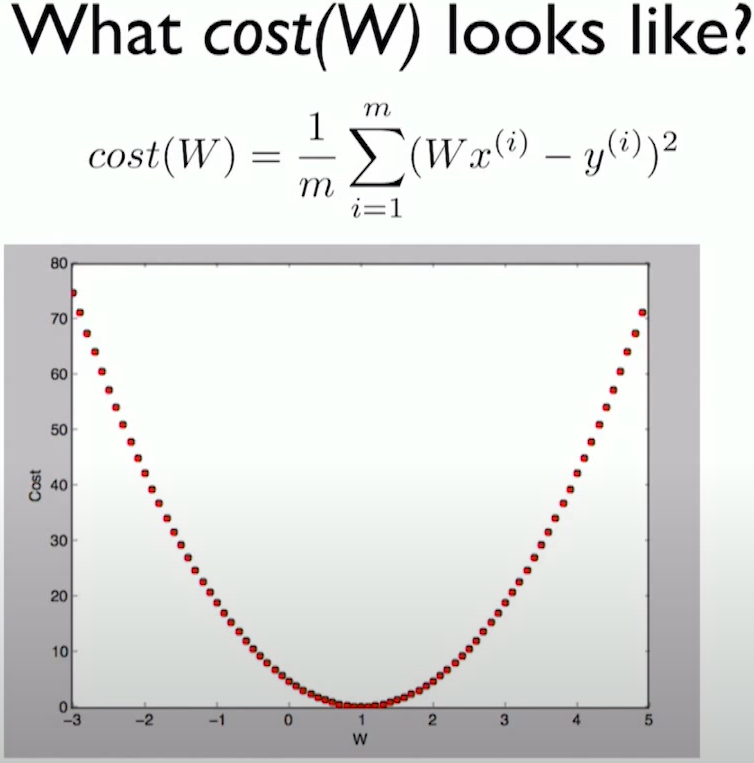
변화하는 W값에 따라 cost값이 변하는 것을 알 수 있다
W = 1일 때 최저점인 것을 알 수 있는데, 예시니까 답이 나온 거지 딥러닝을 학습할 때에는 parameter가 수십만 개에서 수백만 개이다. 수백만 개의 parameter에 따른 cost function을 전부 그릴 수 없다. 이런 상황에서 어떻게 기계적으로 알고리즘을 이용하여 cost를 줄일 것인지 알아내는 방법이 Gradient descent algorithm.
Gradient descent algorithm
- Minimize cost function
- Gradient descent is used many minimization problems
- For a given cost function, cost (W, b), it will find W, b to minimize cost
- It can be applied to more general function: cost(w1, w2, ...)
Gradient descent는 cost function까지 define했고 다양한 W값을 넣어보면서 cost 값이 계산되는 상황인데 어떻게 cost를 줄일 수 있을까에 대한 solution이 될 수 있다
How does it work?
- Start at 0, 0 (or any other value)
- Keeping changing W and b a little bit to try and reduce cost(W, b)
- Each time you change the parameters, you select the gradient which reduces cost(W, b) the most possible
- Repeat
- Do so until you converge to a local minimum
- Has an interesting property
- Where you start can determine which minimum you end up
처음에 랜덤으로 임의의 W부터 시작한다. W는 parameter이고, 이를 랜덤으로 실제로 많이 initialize(초기화)
Ex) 랜덤하게 W = 4에서 시작하여 해당 cost 값을 파악한 뒤 W = 4 + 입실론 정도의 지점에서 다시 한 번 cost 값을 파악.이런 식으로 반복하여 cost 값을 줄이는 방향으로 탐색해 나가는데, 이것이 gradient descent이다
정리하자면 hypothesis를 임의로 랜덤하게 잡고 옆의 것과 비교했을 때 W를 증가시킬지 감소시킬지 판단하여 그 쪽으로 값을 조금씩 바꾸는 것의 무한반복이라 볼 수 있다

그런데 gradient descent 방법은 수치해석적으로 계산했을 때 문제가 많이 발생하여 실제로는 편미분을 통하여 값을 바로 알아낼 수 있다. 또한 수치해석적으로 분석하면 소수점에 대한 문제들이 발생하여 처음부터 편미분한 공식을 가지고 있으면 해당 값에 W에 값을 대입하면 바로 gradient 값을 얻을 수 있다
위 식에서는 미분할 때 제곱의 2가 내려오기 때문에 상쇄되도록 하기 위해 분모에 2를 미리 넣어놓은 것이다

최종적으로 W는 마지막 수식처럼 업데이트될 것이다. 이것이 parameter를 업데이트하는 알고리즘이다
여기서 우리가 구해야할 것은 라운드 loss function이다

위 수식들은 미분하고 정리된 식의 과정이다
정리하자면 linear regression에서 Wx라는 모델에 대해 편미분하여 이에 대해 update rule을 작성할 수 있다

위는 update algorithm을 수식화한 것이다.
Multivariable linear regression
변수가 n개까지 들어오는 상황을 어떻게 처리할 것인가?
Recap
- Hypothesis
- Cost function
- Gradient descent algorithm

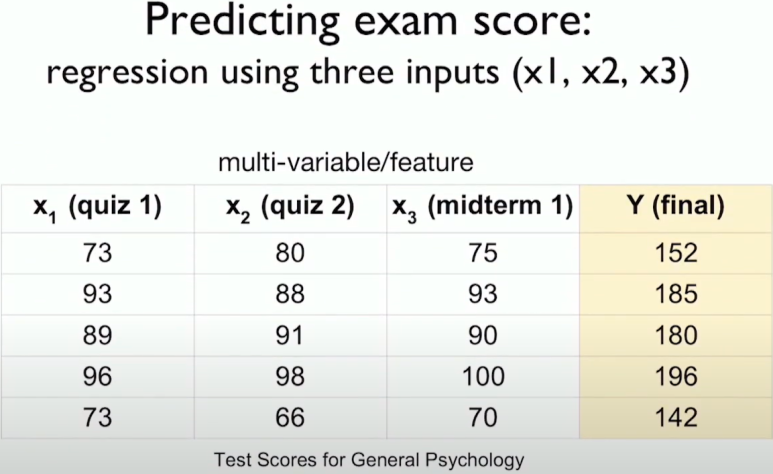
여기서 x는 3차원, y는 1차원이다
Hypothesis
H(x) = Wx + b
이러한 상황에서 linear model을 쓸 것이기에 식은 위와 같이 잡자.

차원이 높아져 식이 늘어났다

이에 따른 cost function
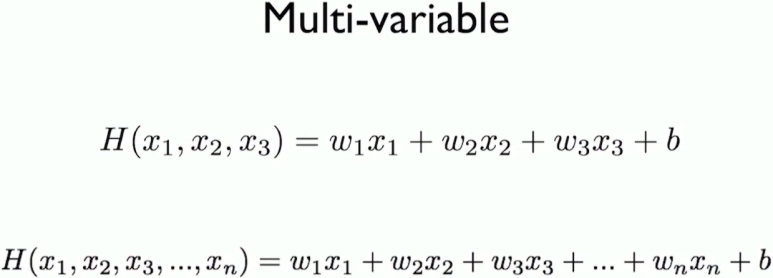
input이 n차원 벡터일 경우에는 위와 같이 표현된다(원래 1차원 벡터였음을 상기하자).


위 수식을 algebric operation으로 표현하면 중간과 같은데, H(X) = XW로 모델이 예측한 값을 표현할 수 있기 때문이다
수식에서 b를 더해준다면 H(X) = XW + B 와 같이 표현될 수 있다

매우 간결하게 표현되는 것을 볼 수 있다 :)